1.1. 시작하기전에
NMEA 0183 (시간, 위치, 방위 등의 정보를 전송하기 위한 규격)은 시간, 위치, 방위 등의 정보를 전송하기 위한 규격입니다. 주로 자이로컴퍼스, GPS, 나침반, 관성항법장치(INS)에 사용되며 ASCII와 직렬 방식의 통신을 사용하도록 고안되었습니다.
NMEA 0183은 3가지 레이어로 구성되어 있으며, 이것은 각각 물리 계층, 데이터링크 계층, 애플리케이션 계층으로 분류됩니다.
NMEA 0183은 3가지 레이어로 구성되어 있으며, 이것은 각각 물리 계층, 데이터링크 계층, 애플리케이션 계층으로 분류됩니다.
- 물리 계층은 RS-232, RS-422 등의 전기적인 전송 규격을 뜻합니다.
- 데이터링크 계층은 Baud rate, Data bit, Parity bit, Stop bit 등이 있습니다.
- 애플리케이션 계층은 데이터를 전송하는 Sentence에 대한 규약입니다.
- 지도 : 3차원의 지구표면을 평면상에 표현한 그림
- 좌표계 : 공간 상의 한 점의 위치를 나타내기 위한 일종의 규칙(약속)으로서 수학적 체계이다.
- 지심좌표계 : 3차원 직각좌표계
- 경위도좌표계 : 적도와 본초자오선의 교점을 원점으로 하는 구면좌표계로서, 원점을 중심으로 적도를 따라 동서로 180˚씩 나누고(경도), 원점을 중심으로 자오선을 따라 남북으로 90˚씩 나누어(위도) 원점을 기준으로 지구중심으로부터 남북/동서 방양의 각도 혹은 적도 및 자오선상의 호의 길이로 위치를 표시한다. 임의로 원점을 지정할 수 있는 직교좌표계와 달리 단일 원점을 가지는 절대좌표계 이다.
- 직교좌표계(직각좌표계, MBRG: Map Based Rectanglar Grid) : 임의의 원점을 지정하고(통상 투영의 원점을 원점으로 지정한다) 원점으로부터 동서방뱡과 남북방향의 거리(m)로 평면상의 위치를 표시하는 2차원 좌표계. TM좌표계, UTM좌표계도 직교좌표계의 일종이다. 좌표계에 음수가 출현하는 것을 방지하기위해 원점으로부터의 북향가산값(False Northing)과 동향가산값(False Easting)을 사용하기도 한다. 사용자가 임의로 원점을 지정하여 사용하는 직교좌표계를 User Grid라한다. 직교좌표계의 명칭은 투영법의 명칭을 그대로 사용하는 경우가 많다.(예: TM좌표계, UTM좌표계)
- 2009년 12월 10일 부터 시행되고 있는 우리나라의 직교좌표계(2009 TM)은 원점을 다음과 같이 각각 정하고 동향가산값은 200,000m, 북향가산값은 600,000m 로 부여하였다. 이전에는 북향가산값이 500,000m(제주도 및 인근 섬의 경우는 550,000m)였으나 600,000m로 통일/변경되었다.
- 서부원점 : 38˚ 00˙ 00˝ N, 125˚ 00˙ 00˝ E
- 중부원점 : 38˚ 00˙ 00˝ N, 127˚ 00˙ 00˝ E
- 동부원점 : 38˚ 00˙ 00˝ N, 129˚ 00˙ 00˝ E
- 동해원점 : 38˚ 00˙ 00˝ N, 131˚ 00˙ 00˝ E
- 2009년 12월 10일 부터 시행되고 있는 우리나라의 직교좌표계(2009 TM)은 원점을 다음과 같이 각각 정하고 동향가산값은 200,000m, 북향가산값은 600,000m 로 부여하였다. 이전에는 북향가산값이 500,000m(제주도 및 인근 섬의 경우는 550,000m)였으나 600,000m로 통일/변경되었다.
- UTM(Universal Tranverse Mercator)는 전 지구상의 위치를 통일된 체계로 나타내기 위해 미육군이 1947년에 개발한 직교좌표계 방식으로서 TM 투영을 그 기본으로 하는데, 북위 84도에서 남위 80도 사이의 지역을 경도 180˚를 기준으로 경도 6˚ 폭으로 구획하여 서경 180˚ ~ 174˚ 구역(Zone)을 1번으로하여 동쪽으로 향하며 구역번호를 부여하고 (동일한 좌표가 북반구와 남반구에 두개 존재하게 되므로 구분할 수 있도록)적도를 기준으로하여 위도 8˚ 폭(단 가장 북쪽의 N72˚~N84˚ 구역은 12˚ 폭)으로 구획하여 북반구는 N~X 남반구는 M~C 의 구역기호(I와 O는 사용하지 않음)를 부여하여 구역번호와 구역기호를 조합하여 구역명칭으로 한다. 구역마다 중심자오선을 취하여 투영하며 각 구역의 중앙자오선과 적도의 교점을 원점으로 하여 m단위로 위치를 표시하는데(주의: 구역기호에 따른 원점변경은 없음, 즉 같은 구역번호를 가진 구역은 원점이 동일) 좌표에 -값이 사용되는 걸 방지하기 위하여 동향(Easting)값에는 500,000 남반구의 북향(Northing)값에는 10,000,000을 더하여 표시한다. UTM 투영에서는 중심자오선과 평행한 남북방향으로의 scale 왜곡은 일정하지만 중심자오선으로 부터 동쪽이나 서쪽으로 멀어질 수록 Scale 왜곡이 심하게 되므로 왜곡을 동일하게 하기 위하여, 측정된 모든 길이에 대하여 Scale factor(축척계수 또는 선증대율) 0.9996을 곱해준다. UTM 좌표계와 경위도 좌표계 간의 좌표계 변환시에는 이 값을 적용하여야 한다.(중앙자오선에서 동서방향으로 약 180Km 지점에서 선확대율이 1.0000이 되고 중앙자오선상의 선확대율은 0.9996이 된다. 따라서 중앙자오선상에서의 수평오차는 180,000 x (1-0.9996)=72m가된다. 북위 84도에서 남위 80도 이외의 지역은 UPS(Universal Polar Stereographic) 투영법으로 지도를 제작한다. 군용지도의 좌표계인 MGRS(Military Grid Reference System)은 이 UTM 좌표계를 바탕으로 만들어지는데, UTM 좌표계 그자체라고도 생각할 수 있다.(UTM 좌표계의 각 구역을 가로세로 각100KM로 구획하여 각각의 구역에 알파벳 두자리의 구역기호를 부여하고 UTM구역원점으로 부터의 거리 좌표를 사용, 좌표값이 UTM 좌표에서 끝의 5자리 숫자와 동일)
- UTM-K : 2004년 6월 15일에 건설교통부(현, 국토해양부)에서 "한국형 UTM좌표계"라고 명명하여 고시한 직교좌표계로서 원점을 동경 127˚ 30' 00.000˝ 북위 38˚ 00' 00.000˝로 정하고 동향가산값을 1,000,000m 북향가산값을 2,000,000m 로 부여하였으며 이외의 사항은 UTM과 동일하다. 기존 TM좌표계에서는 지역에 따라 서부, 중부, 동부, 동해 원점을 각각 사용하였으나, 전국 단위의 연속적인 기본 지리 정보의 위치 기준을 통일함으로서 분야별 기본 지리 정보와 여러 GIS를 상호 연계, 통합하기 위해 하나의 원점을 가지는 단일평면직각좌표계를 제정하였다고 한다.
- Geoid : 평균해수면(조석이 없다고 가정했을 때의 해수면)을 육지까지 연장한 곡면에 중력을 고려하므로 밀도가 높은 곳은 볼록하게 밀도가 낮은 곳은 오목하게 나타난다. 준거타원체는 이 Geoid에 가장 근사하게 정의한다.
- 준거타원체(準據楕圓體, Reference Ellipsoid) : 형상이 불규칙하여 계산이 불가능한 실제의 지구를 대체하여 계산이 가능하도록 실제지구의 형상과 가장 가깝게 수학적 으로 규격을 정의한 가상의 타원체로서 여러 가지가 있으며, 가상지구타원체 라고도 한다. 준거타원체는 물리적 표면과 Geoid 면에 근사하는 조건을 가지고 있어야 하며 중심축과 중심은 Geoid의 중심과 회전축에 일치한다.
- 수준원점(OBM, Original bench mark) : 고도의 기준원점은 검조장에서 다년간 조석 관측한 결과를 평균조정한 평균해수면(MSL, Mean sea level)인데, 이 평균해수면은 일종의 가상면으로 수준 측량에 직접 사용할 수 없으므로 평균해수면을 기준으로 계산하여 육상에 설치한 고도의 기준이되는 원점. 현재 사용하고 있는 우리나라의 수준원점은 인하공업전문대학 교정 내에 설치되어 있으며, 인천만의 평균 해면상으로부터 26.6871m 고도에 존재한다. 따라서 수준원점으로 부터의 고도가 100m 라면 실제 고도는 126.6871m가 된다. 참고로 수심의 기준은 가장 낮은 수준면인 기준수준면인데, 가장 얕을 때의 수심을 표시하여 선박통항의 안전을 도모하기위해서이다.
- WGS84(World Geodetic System 1984) : 미국방성에서 군사 및 GPS 운영을 목적으로 규정한 타원체. WGS60, WGS66, WGS72 타원체를 거쳐 현재는 민간과 타원체를 통합하기위해 1984년에 정의한 타원체인 WGS84(장반경: 6378137.0m, 단반경: 6356752.3142m, 1/298.257)를 사용하고 있다. GPS 수신기는 GPS위성으로 부터 신호를 수신하여 이 WGS84 타원체에 근거한 위치를 계산하여 알려준다.
- GRS80(Geodetic Reference System 1980) : 국제측지학협회(IAG - International Association of Geodesy) 와 국제측지학 및 지구물리학연합(IUGG - International Union of Geodesy and Geophysics)에서 1979년에 채택(정의)한 타원체(장반경: 6378137.0m, 단반경: 6356752.3141m). 국제지구회전관측사업(IERS)라고하는 국제적인 학술 기관이 구축하고 있는 3 차원 직교좌표계인 국제지구기준 좌표계(ITRF - International Terrestrial Reference Frame)에서 채택하고 있다. 현재 지구를 가장 잘 나타내고 있는 타원체로서 널리 이용되고 있다.
- Bessel1841 : 독일의 과학자 Bessel이 1841년에 개발(정의)한 타원체(장반경 : 6,377,397.2m, 단반경 : 6,356,079.0m, 편평율 : 1/299.15) Tokyo 측지계에서 채택하고 있다.
- 측지계(Datum) : 준거타원체를 수학적으로 정의한 값(원점요소, 장반경, 단반경, 평편률, 이심률) 및 타원체 원점의 위치값을 포함하여 지리 위치를 정의하기위한 여러가지 수학적 공식과 데이터의 집합으로서 포괄적 의미를 지닌다.(역으로 이야기하자면 위치좌표값의 산출근거, 예: WGS84 데이텀, Tokyo 데이텀 등) Bessel 1841 타원체를 채택한 측지계의 경우, 타원체는 동일하지만 나라마다의 지리적 특성에 맞춰 타원체의 중심위치를 변경하여 타원체의 표면이 그 지역의 지표면을 통과하도록 수정한다든지 하여 사용하고 측지계의 명칭도 달리 사용한다. 또 수평기준원점과 수직기준원점을 각각 수평데이텀, 수직 데이텀 으로 부르기도 하는 것 같다.
- 지축(Axis of the Earth) : 지구의 회전축, 양끝을 지구의 양극(남극, 북극)이라 하며, 북극 방향이 진북 방향이다. 지구의 양극과 지자기의 극은 일치하지 않는데, 이 차이를 편차(Variation, V)라한다. 즉 편차란 진자오선 과 자기자오선이 이루는 교각을 의미한다. 또 지자기의 극은 고정되어 있지 않고 960년을 주기로 진극을 중심으로 이동하기때문에 편차는 장소와 시간의 경과에 따라 변한다. 지도의 난외주기에 진북, 자북 도북의 차이가 기재되어 있다.
- 大圈(Great Circle) : 지구의 중심을 중심점으로 하고 원주가 지구의표면에 접하는 원(다른 말로 표현하자면 지구표면에 작도할 수 있는 원 중에서 중심점이 지구의 중심인 원)으로서 지구상에 무수히 존재한다. 지구상의 두지점사이의 가장 짧은 거리는 두지점을 연결하는 대권의 호의 길이이다. 대권항해란 여기서 비롯된 항법.
- 子午線(Merdian) : 대권중에서 지구의 양극을 지나는 선. 적도와 직교하며 무수히 많이 존재한다. 그중에서 영국의 그리니치(Greenwich) 천문대를 통과하는 자오선을 0˚로 하여 경도의 기준으로 삼고 본초자오선(Prime Meridian)이라고 한다. 경도란 본초자오선과 어느 지점을 통과하는 자오선이 지구중심에서 이루는 각도 또는 적도상의 호의 길이. 경도 180˚ 선은 날짜 변경선이라하여 서쪽에서 동쪽으로 넘으면 하루를 빼고(같은 날짜 반복) 동쪽에서 서쪽으로 넘으면 하루를 더한다.(하루를 건너뜀) 경도는 각도 대신 시간으로 표시하는 경우도 있는데, 경도 15°는 1시간, 15'은 1분, 15"는 1초에 해당한다. 따라서 어떤 지점의 지방시(地方時)와 그리니치시(時)의 시차로 그 지점의 경도를 알 수 있다. 옛날의 항해자들은 그리니치시에 맞춘 시진의(Chronometer, 정밀한 시계)의 시각과 천문관측으로 측정한 지방시를 비교해서 그 지점의 경도를 구하였다. 위도는 야간에 북극성의 고도를 측정하여 알아내었다. 지구상공에 인공위성이 떠 있는 오늘날에도 해상에서는 숙달된 항해사가 육분의로 별의 고도와 방위각을 측정하고 그 측정값을 바탕으로 AlManac을 이용하여 산출한 위치가 GPS가 알려주는 위치보다 정확한 경우도 왕왕 있으므로 구식방법이라고 무시하지 못함.
- 赤道(Equator) : 대권중에서 지축과 직교하는 원. 하나만 존재한다. 위도 0˚
- 小圈(Small Circle) : 지구의 표면에 원주가 접하는 대권 이외의 원으로서 이 역시 무수히 존재한다.
- 거등권(Parallel) : 무수히 많은 소권중에 적도와 평행한 소권. 위도선. 위도에는 지리위도, 지심위도, 천문위도가 있는바, 지리위도는 어떤 지점에서 지표면에 수직인 직선이 적도면과 이루는 각도를 말하며 지심위도는 그 지점을 지구중심과 연결한 직선이 지구중심에서 적도면과 이루는 각도이고 천문위도는 그지점에서의 수준면에 대한 연직선이 지구의 자전축과 이루는 각도인데 천체를 관측하여 결정한다. 지심위도와 천문위도의 차는 몇초정도로 미소하지만 지리위도와 지심위도의 차이는 가장 클 때 11˙ 30˝ 이다. 또 지도에 사용되는 위도는 지리위도 이다.
- 圖法 : 3차원의 지구표면을 평면상에 나타내는 방법, 즉 지도의 제작방법을 의미하는데, 상상으로 지구를 투명한 구로 가정하고, 중심에서 지구의 표면 또는 한점에 접한 스크린에 빛을 투사하여 스크린에 나타나는 영상을 취하는 방법을 사용하므로 투영도법(Method of Projection) 또는 투영법(Projection, Map Projection)이라고도 한다. 상상속에서 스크린은 지구표면에 접하는 꼬깔(Cone), 원통(Cylinder) 또는 지구표면의 한 점에 접하는 평면(Plane) 등으로 가정하는데, 가정하는 스크린에 따라 표현되는 지구의표면의 모양(지도)가 달라지게되므로 지도를 제작할 지역의 실제지형을 최소의 왜곡으로 나타낼 수 있는 스크린을 채택(도법선택)하게 된다.
- 정거도법(正距圖法): 투영면상의 거리가 일정한 도법, 기본지형도
- 정적도법(正積圖法): 투영면상의 면적이 일정한 도법, 각종 분포도
- 정각도법(正角圖法): 투영면상의 방위각이 일정한 도법, 항행도
- 심사도법(Gnomonic Projection)은 스크린으로 지구표면의 한점에 접하는 평면을 가정하고 그 평면위에 지구표면을 투영하는 투영법인데 항해관계에서는 大圈圖法(Great Circle Projection)이라는 용어를 주로 사용한다.
- 자오선(경선, 子午線) : 지구의 남극과 북극을 연결하는 지표상의 가상선으로 경도를 표시할 때 사용됩니다.
- 위선 : 적도에 평행하게 지구 둘레를 따라 그은 가상적인 선으로, 위도를 나타내는 데 사용됩니다.
- 위도(緯度, 씨줄, Latitude)
- 적도를 기준으로 북쪽 또는 남쪽으로 얼마나 떨어져 있는지 나타내는 위치입니다.
- 북위(N)는 "+", 남위(S)는 "-" 로 다룹니다.
- 위도에서 가장 큰 값은 북위 90°와 남위 90°가 됩니다. (양 극으로 갈수록 위도가 높아집니다.)
- 위도 1°간의 거리는 균일합니다.
- 경도(經度, 날줄, Longitude)
- 본초 자오선을 기준으로 동쪽 혹은 서쪽으로 얼마나 떨어져 있는지 나타내는 위치입니다.
- 동경(E)는 "+", 서경(W)는 "-" 로 다룹니다.
- 육분의 시절부터 전해내려온 전통으로 인해 영국의 그리니치 천문대가 있던 자리가 기준이 됩니다. 그러나 현재의 그리니치 천문대는 런던의 광공해를 피해 다른 지역으로 이전했으며, 천문대가 이전했다고 경도의 기준선까지 바꾸는 것은 혼란스럽기 때문에, 여전히 구 천문대 터가 기준선이 됩니다.
- 시간 계산 경도 0°에서 동쪽으로 15°이동할 때마다 1시간 빨라집니다. (대한민국의 표준 경선은 동경 135°이며 이에 따라서 0°를 표준 경선으로 사용하는 영국보다 +9시간 빠릅니다.)
- 날짜 변경선 : 서경 180°와 동경 180°가 만나는 지점에서 날짜가 달라지는 문제(24시간의 시차 발생)를 해결하기 위해 설정한 가상의 선입니다.
- 날짜 변경선의 동쪽이 서쪽보다 하루가 느리다고 할 수 있습니다.
- 경도간의 거리는 위도에 따라서 다릅니다. 극지방으로 갈수록 경도간의 거리는 짧아집니다.
- DMS(Degree Minutes Seconds)
- DD(Decimal Degree)
- 노트(kn, knot
[s]) - 해리(海里, nautical mile, nmile)
1.2. 지구(地球, Earth) 의 반지름
- 적도(赤道, Equator)반지름 : 약 6,378.1 km
- 극(極)반지름 : 약 6,356.7 km
- 지구의 평편도/평편률(偏平度, Flattening) : (적도반지름 - 극반지름) / 적도반지름 = 약 1/298.3
- 지구는 거의 둥글다고 할 수 있습니다. 하지만 엄밀하게는 아주 약간 위-아래 에서 눌러 놓은것처럼 생겼습니다. 그리고 북극이 남극보다 약간 튀어나온 형상이라고 합니다.
1.3. 경위도 좌표계의 변환
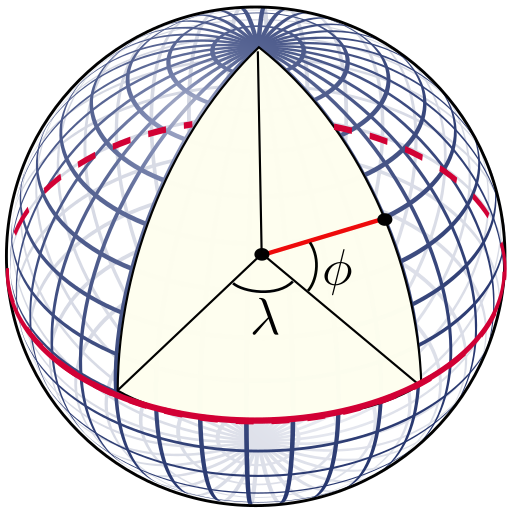 [PNG image (231.08 KB)] |
![[https]](/moniwiki/imgs/https.png) 이미지 출처(wikipedia) 이미지 출처(wikipedia)![[]](/moniwiki/imgs/moni2/external.png) |
- DMS(Degree Minutes Seconds) 단위를 DD(Decimal Degree) 단위로 변환
"도(D)", "분(M)", "초(S)" 를 각각 D, M, S 로 저장하고 다음과 같이 계산을 도출할수 있습니다. DD = D + (M / 60) + (S / 3600)
- DD(Decimal Degree) 단위를 DMS(Degree Minutes Seconds) 단위로 변환
D = int(DD) /* DD(Decimal Degree)의 정수부만 취함 */ TEMP = (DD - D) * 60 /* DD(Decimal Degree)의 소수부에 60을 곱함 */ M = int(TEMP) /* TEMP의 정수부만 취함 */ S = (TEMP - D) * 60 /* TEMP의 소수부에 60을 곱함 */
- 예1) 아래의 그림은 시청앞 세종대왕동상의 위치를 구글지도에서 찾아본겁니다. 여기서 "37°34'22.2"N 126°58'36.9"E" 가 "WGS84 / DMS(Degree Minutes Seconds) 단위"에 해당되고 "37.572839, 126.976915" 가 "WGS84 / DD(Decimal Degree) 단위" 에 해당됩니다. DMS(Degree Minutes Seconds) 단위와 DD(Decimal Degree) 단위간의 변환을 계산해보세요. (이 좌표를 구글맵을 인용하여 표시하면 아래의 이미지가 가르키는 "A" 지점이 됩니다.)
- 예2) DD(Decimal Degree) 단위의 두 좌표간의 거리계산 (Google map API 방식)
#define def_hwport_pi (3.14159265358979323846) double s_earth_round; double s_radian; double s_lat[2]; double s_lon[2]; double s_lat_radian[2]; double s_lon_delta_radian; double s_distance; double s_result; /* 지구의 추상화된 구형의 반지름 */ s_earth_round = 6371000.0; s_radian = def_hwport_pi / 180.0; /* 서울특별시청 위치 */ s_lat[0] = 37.566788; /* 위도 */ s_lon[0] = 126.978039; /* 경도 */ /* 부산시청 위치 */ s_lat[1] = 35.180202; /* 위도 */ s_lon[1] = 129.075388; /* 경도 */ /* 단위를 라디안(radian)으로 변환 */ s_lat_radian[0] = s_lat[0] * s_radian; s_lat_radian[1] = s_lat[1] * s_radian; s_lon_delta_radian = (s_lon[0] - s_lon[1]) * s_radian; s_distance = sin(s_lat_radian[0]) * sin(s_lat_radian[1]); s_distance = s_distance + cos(s_lat_radian[0]) * cos(s_lat_radian[1]) * cos(s_lon_delta_radian); s_result = round(s_earth_round * acos(s_distance)); (void)fprintf(stdout, "%f m\n", s_result); /* 이 예제에서는 대략 "서울특별시청"과 "부산시청"간의 거리는 325km로 나옵니다. */
- 예3) DD(Decimal Degree) 단위의 두 좌표간의 거리계산 (피타고라스의 정리만을 단순히 적용한 방식)
#define def_hwport_pi (3.14159265358979323846) double s_earth_radius[2]; double s_earth_distance[2]; double s_lat[2]; double s_lon[2]; double s_lat_delta; double s_lon_delta; double s_lat_distance; double s_lon_distance; double s_result; /* 지구의 반지름 */ s_earth_radius[0] = 6356700.0; /* 극(極)반지름 */ s_earth_radius[1] = 6378100.0; /* 적도(赤道, Equator)반지름 */ /* 지구의 둘레 (2pi * R) */ s_earth_distance[0] = s_earth_radius[0] * (2.0 * def_hwport_pi); s_earth_distance[1] = s_earth_radius[1] * (2.0 * def_hwport_pi); /* 서울특별시청 위치 */ s_lat[0] = 37.566788; /* 위도 */ s_lon[0] = 126.978039; /* 경도 */ /* 부산시청 위치 */ s_lat[1] = 35.180202; /* 위도 */ s_lon[1] = 129.075388; /* 경도 */ /* 위도, 경도 각각의 변위값 */ s_lat_delta = (s_lat[0] >= s_lat[1]) ? s_lat[0] - s_lat[1] : s_lat[1] - s_lat[0]; s_lon_delta = (s_lon[0] >= s_lon[1]) ? s_lon[0] - s_lon[1] : s_lon[1] - s_lon[0]; /* 미터단위로 변환 */ #if 0L /* 위도에 따른 경도간의 거리는 다르기 때문에 이 부분은 적도지역에서만 유효한 공식입니다. */ s_lat_distance = (s_lat_delta * s_earth_distance[0]) / 360.0; s_lon_distance = (s_lon_delta * s_earth_distance[1]) / 360.0; #else /* 대한민국이 위치한 위도 37°만을 고려한 경도 1°간의 거리를 기준으로 계산하는 방법입니다. (위도에 따른 경도간의 거리를 산출할수 있다면 보다 개선될수 있겠죠.) */ s_lat_distance = (s_lat_delta * s_earth_distance[0]) / 360.0; s_lon_distance = s_lon_delta * 88907.949 /* 위도 37°에서 경도 1°간의 거리는 약 88907.949m 로 계산하였습니다. */; #endif /* 피타고라스의 정리에 따른 삼각형 dx(경도의 변위 거리), dy(위도의 변위 거리)를 가지고 distance(거리)를 구합니다. (distance^2 = dx^2 + dy^2) */ s_result = round(sqrt(pow(s_lat_distance, 2.0) + pow(s_lon_distance, 2.0))); (void)fprintf(stdout, "%f m\n", s_result); /* 이 예제에서는 대략 "서울특별시청"과 "부산시청"간의 거리는 324km로 나옵니다. */ /* IMPORTANT!!! 지구는 둥글고 위도간 경도의 거리는 차이가 있기 때문에 극지방에 가까워지거나 위도의 차이가 큰 지점간의 계산은 이 방법으로는 오차가 커지게 됩니다. 하지만 대한민국 정도의 내륙땅에서의 지점간 거리는 그 오차가 무시할 수준으로 볼수도 있기에 활용할수 있는 방법이기도 합니다. */
- 예4) WGS84 좌표로 이루어진 두 좌표간의 거리를 미터(m)단위로 반환하는 JavaScript 함수의 구현
function hwport_wgs84_degree_distance(s_latitude1, s_longitude1, s_latitude2, s_longitude2) { var def_hwport_pi = 3.14159265358979323846264338327950288; var cg_earth_round = 6371000.0; var s_latitude_radian1; var s_latitude_radian2; var s_longitude_delta_radian; var s_distance; s_latitude_radian1 = s_latitude1 * def_hwport_pi / 180.0; s_latitude_radian2 = s_latitude2 * def_hwport_pi / 180.0; s_longitude_delta_radian = (s_longitude1 - s_longitude2) * def_hwport_pi / 180.0; s_distance = Math.sin(s_latitude_radian1) * Math.sin(s_latitude_radian2); s_distance = s_distance + Math.cos(s_latitude_radian1) * Math.cos(s_latitude_radian2) * Math.cos(s_longitude_delta_radian); return(cg_earth_round * Math.acos(s_distance)); }
- 예5) WGS84 좌표로 이루어진 두 좌표간의 거리를 미터(m)단위로 반환하는 SQL Query 문
SELECT ROUND( 6371000.0 * ACOS( COS(RADIANS(latitude1)) * COS(RADIANS(latitude2)) * COS(RADIANS(longitude2) - RADIANS(longitude1)) + SIN(RADIANS(latituide1)) * SIN(RADIANS(latitude2)) ), 2) AS distance ...;
1.4. 속도를 나타내는 노트(kn, knot[s]) 와 km/h 간의 단위 변환
- 노트(kn, knot
[s])는 줄에 매듭을 지어 바다로 던져 1시간동안 움직인 거리를 측정한 것에서 유래되었습니다. - 해리(海里, nautical mile, nmile)는 자오선(子午線)의 위도(緯度) 1°(도)의 평균거리를 말합니다. 1929년에 국제수로국에서 정의한 1해리(海里, nautical mile, nmile)는 1,852m(6076.12 feet) 입니다. 영국의 경우는 1,853.184m (6080 feet)로 정의합니다.
- 노트(kn, knot
[s])는 바다나 공중에서 사용하는 속도의 단위로서, 선박이나 항공기가 1시간에 1해리(海里, nautical mile, nmile, 약 1,852m)만큼 가는 속도를 1kn(1nmile/h) 라고 합니다. - 상호간 변환에는 다음과 같은 공식이 성립합니다.
1knot(kn) = 1nmile/h = 1.852km/h
1.5. 프로토콜 메세지 형식 (NMEA Protocol Message Format)
| STX($, 24H) | Checksum range | ETX(*, 2AH), Checksum | End of message indicator (0DH, 0AH) | |
| $ | Address, | {<value>} | *<checksum> | <CR><LF> |
- message 예시 ("=>" 표시 라인은 구문해석의 예)
$GPGGA,071448.00,3730.96956,N,12705.87558,E,1,04,1.71,31.7,M,18.7,M,,*6E => 07:14:48.000000, 37.5161593333,127.0979263333, Calc=4, HDOP=1.71000000, Alt=31.70000000M, DiWGS84=18.70000000M $GPGSA,A,3,23,26,31,27,,,,,,,,,6.26,1.71,6.02*01 $GPGSV,3,1,09,09,22,313,,16,64,311,,19,19,204,,21,21,080,*72 $GPGSV,3,2,09,23,42,286,18,26,63,028,22,27,52,198,29,29,01,037,*7F $GPGSV,3,3,09,31,43,114,25*46 $GPGLL,3730.96956,N,12705.87558,E,071448.00,A,A*63 => 07:14:48.000000, 37.51615933,127.09792633 $GPRMC,071449.00,A,3730.96979,N,12705.87536,E,0.505,,230415,,,A*7F => 07:14:49.000000, 37.51616317,127.09792267, 0.93526000 km/h, 2015/04/23 $GPVTG,,T,,M,0.505,N,0.935,K,A*2C $GPGGA,071449.00,3730.96979,N,12705.87536,E,1,04,1.71,31.7,M,18.7,M,,*6A => 07:14:49.000000, 37.5161631667,127.0979226667, Calc=4, HDOP=1.71000000, Alt=31.70000000M, DiWGS84=18.70000000M $GPGSA,A,3,23,26,31,27,,,,,,,,,6.26,1.71,6.02*01 $GPGSV,3,1,09,09,22,313,,16,64,311,,19,19,204,,21,21,080,*72 $GPGSV,3,2,09,23,42,286,17,26,63,028,22,27,52,198,29,29,01,037,*70 $GPGSV,3,3,09,31,43,114,26*45 $GPGLL,3730.96979,N,12705.87536,E,071449.00,A,A*67 => 07:14:49.000000, 37.51616317,127.09792267 $GPRMC,071450.00,A,3730.96983,N,12705.87534,E,0.544,,230415,,,A*75 $GPVTG,,T,,M,0.544,N,1.008,K,A*2F $GPGGA,071450.00,3730.96983,N,12705.87534,E,1,04,1.71,31.8,M,18.7,M,,*6A $GPGSA,A,3,23,26,31,27,,,,,,,,,6.26,1.71,6.02*01 $GPGSV,3,1,09,09,22,313,,16,64,311,,19,19,204,,21,21,080,*72 $GPGSV,3,2,09,23,42,286,15,26,63,028,22,27,52,198,29,29,01,037,*72 $GPGSV,3,3,09,31,43,114,26*45 $GPGLL,3730.96983,N,12705.87534,E,071450.00,A,A*68 $GPRMC,071451.00,A,3730.96982,N,12705.87530,E,0.175,,230415,,,A*77 $GPVTG,,T,,M,0.175,N,0.324,K,A*25 $GPGGA,071451.00,3730.96982,N,12705.87530,E,1,04,1.71,31.6,M,18.7,M,,*60 $GPGSA,A,3,23,26,31,27,,,,,,,,,6.26,1.71,6.02*01 $GPGSV,3,1,09,09,22,313,,16,64,311,,19,19,204,,21,21,080,*72 $GPGSV,3,2,09,23,42,286,12,26,63,028,22,27,52,198,29,29,01,037,*75 $GPGSV,3,3,09,31,43,114,26*45 $GPGLL,3730.96982,N,12705.87530,E,071451.00,A,A*6C $GPRMC,071452.00,A,3730.96953,N,12705.87530,E,0.441,,230415,,,A*7A $GPVTG,,T,,M,0.441,N,0.818,K,A*23 $GPGGA,071452.00,3730.96953,N,12705.87530,E,1,04,1.71,31.6,M,18.7,M,,*6F $GPGSA,A,3,23,26,31,27,,,,,,,,,6.25,1.71,6.02*02 $GPGSV,3,1,09,09,22,313,,16,64,311,,19,19,204,,21,21,080,*72 $GPGSV,3,2,09,23,42,286,14,26,63,028,22,27,52,198,29,29,01,037,*73 $GPGSV,3,3,09,31,43,114,26*45 $GPGLL,3730.96953,N,12705.87530,E,071452.00,A,A*63 $GPRMC,071453.00,A,3730.96959,N,12705.87499,E,0.195,,230415,,,A*7F $GPVTG,,T,,M,0.195,N,0.362,K,A*29
1.6. 참고자료
![[http]](/moniwiki/imgs/http.png) NMEA home-page
NMEA home-page![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://nmea.sourceforge.org.net/
http://nmea.sourceforge.org.net/![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://ko.wikipedia.org/wiki/NMEA
http://ko.wikipedia.org/wiki/NMEA![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://nmea.sourceforge.net/
http://nmea.sourceforge.net/![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://linuxism.tistory.com/m/post/833?hc_location=ufi
http://linuxism.tistory.com/m/post/833?hc_location=ufi![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://blog.naver.com/conso1e/220052928322
http://blog.naver.com/conso1e/220052928322![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://www.biz-gis.com/?mid=GISFAQ&page=3&document_srl=12110
http://www.biz-gis.com/?mid=GISFAQ&page=3&document_srl=12110![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) 좌표계 관련 설명
좌표계 관련 설명![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) 그리니치 천문대에 대하여
그리니치 천문대에 대하여![[]](/moniwiki/imgs/moni2/external.png)
![[https]](/moniwiki/imgs/https.png) Google Static Maps API V2 개발자 가이드
Google Static Maps API V2 개발자 가이드![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) Daum 지도 API
Daum 지도 API![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://newdle.noonnoppi.com/xmlView.aspx?xmldid=112512
http://newdle.noonnoppi.com/xmlView.aspx?xmldid=112512![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) GIS 분석 전문 사이트 - 비즈GIS
GIS 분석 전문 사이트 - 비즈GIS![[]](/moniwiki/imgs/moni2/external.png)
- 좌표간의 거리를 구하는 방법 및 단위계에 대한 참고자료
![[http]](/moniwiki/imgs/http.png) http://www.movable-type.co.uk/scripts/latlong.html
http://www.movable-type.co.uk/scripts/latlong.html![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://onlybalance.pe.kr/xe/tech/891
http://onlybalance.pe.kr/xe/tech/891![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://www.devpia.com/MAEUL/Contents/Detail.aspx?BoardID=50&MAEULNO=20&no=761133&ref=761126
http://www.devpia.com/MAEUL/Contents/Detail.aspx?BoardID=50&MAEULNO=20&no=761133&ref=761126![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://lovestudycom.tistory.com/71
http://lovestudycom.tistory.com/71![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://en.wikipedia.org/wiki/Nautical_mile
http://en.wikipedia.org/wiki/Nautical_mile![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://autoc.tistory.com/315
http://autoc.tistory.com/315![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://www.biz-gis.com/index.php?document_srl=65754&mid=pds
http://www.biz-gis.com/index.php?document_srl=65754&mid=pds![[]](/moniwiki/imgs/moni2/external.png)
![[http]](/moniwiki/imgs/http.png) http://www.biz-gis.com/index.php?mid=pds&page=2&document_srl=67335
http://www.biz-gis.com/index.php?mid=pds&page=2&document_srl=67335![[]](/moniwiki/imgs/moni2/external.png)
- 지도 서비스
- 주소체계
- 정보제공 서비스
- 수학 (mathematics, 數學) 알고리즘
- 기타정보
