1.1. 개요
Diffie-Hellman 키 분배 방법은 상호간 비밀키를 그대로 교환하지 않고 안전하게 공유할 수 있도록 하는 절차이며 RFC2631(![[https]](/moniwiki/imgs/https.png)
RFC2631 - Diffie-Hellman Key Agreement Method![[]](/moniwiki/imgs/moni2/external.png)
)에 규정되어 있습니다.
하지만 이러한 키 분배 방법만으로는 상대방을 인증(사용자 인증 및 메세지 인증)할 수 있는 기능이 없어Man-in-the-middle attack공격에 취약한 문제점이 존재하며 이를 보완하기 위해서 디지털 서명과 그 밖에 여러수단을 복합적으로 추가수행하는 것이 필요합니다.
RFC2631 - Diffie-Hellman Key Agreement Method)에 규정되어 있습니다.
하지만 이러한 키 분배 방법만으로는 상대방을 인증(사용자 인증 및 메세지 인증)할 수 있는 기능이 없어
Man-in-the-middle attack공격에 취약한 문제점이 존재하며 이를 보완하기 위해서 디지털 서명과 그 밖에 여러수단을 복합적으로 추가수행하는 것이 필요합니다.
1.2. Diffie-Hellman 방식에 의한 키 분배 방법
각 a와 b 상호간에 비밀키 K를 공유하고자 할 때 상호간 미리 알려진 값 p(prime modulus)와 g(generator)값을 가지고 다음과 같이 절차를 진행합니다.
기호 "^" : 거듭제곱
기호 "%" : 나숫셈의 나머지
기호 "^" : 거듭제곱
기호 "%" : 나숫셈의 나머지
- 각 상호간 다음과 같이 Ya, Yb를 생성합니다.
- a가 생성하는 값
- Ra = 임의의 수 random 값
- Xa < p = Ra % p: 개인 값
- Ya = (g ^ Xa) % p : 공개 값
- b가 생성하는 값
- Rb = 임의의 수 random 값
- Xb < p = Rb % p : 개인 값
- Yb = (g ^ Xb) % p : 공개 값
- a가 생성하는 값
- a 와 b는 각자 생성한 공개 값인 Ya와 Yb를 교환합니다.
- 이제 a와 b는 각자가 생성한 값과 교환한 값을 이용하여 Session Key값 K를 생성하여 상호간 공유할 수 있게 됩니다.
- a가 산출하는 Session Key 값 K
- K = (Yb ^ Xa) % p
- b가 산출하는 Session Key 값 K
- K = (Ya ^ Xb) % p
- a가 산출하는 Session Key 값 K
1.2.1. 예시
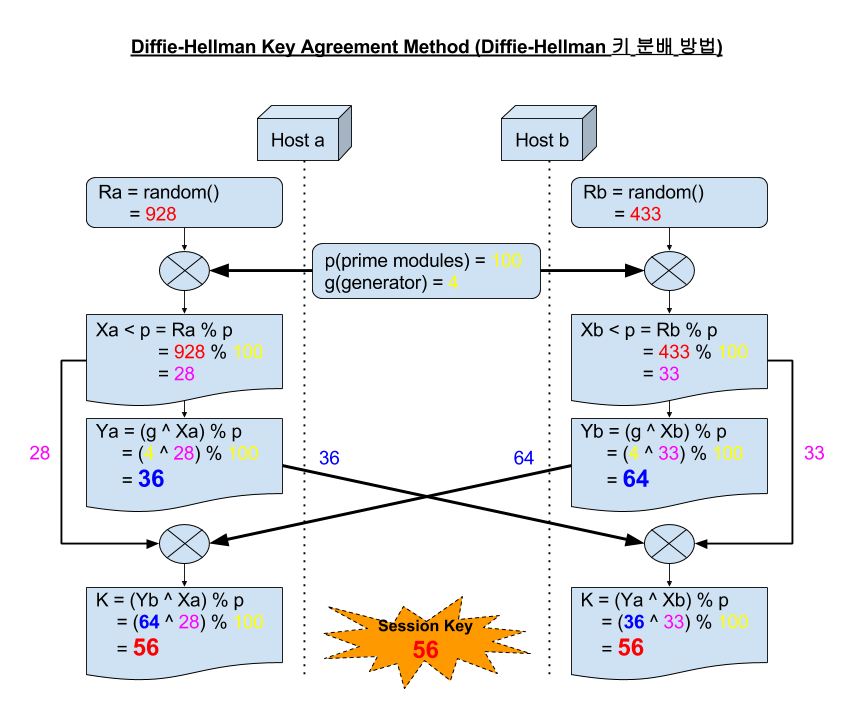
이 방법을 이용한 예를 들어 키 산출한다면 다음과 같습니다. (이 예시에서는 p, g, random 값을 매우 작은 값으로 사용하였으나 실제 보안 장비들에서 구현시에는 매우 큰 값을 사용하게 됩니다.)
[PNG image (67.11 KB)]
- p = 100, g = 4
- a가 생성하는 값
- Ra = random = (임의의 수 Ra 가 928 이라고 할 때)
- Xa = Ra % p = 928 % 100 = 28
- Ya = (g ^ Xa) % p = (4 ^ 28) % 100 = 72057594037927936 % 100 = 36
- b가 생성하는 값
- Rb = random = (임의의 수 Ra 가 433 이라고 할 때)
- Xb = Rb % p = 433 % 100 = 33
- Yb = (g ^ Xb) % p = (4 ^ 33) % 100 = 73786976294838206464 % 100 = 64
- a가 생성하는 값
- a 와 b는 각자 생성한 공개 값인 Ya와 Yb를 교환합니다.
- 이제 a와 b는 각자가 생성한 값과 교환한 값을 이용하여 Session Key값 K를 생성하여 상호간 공유할 수 있게 됩니다.
- a가 산출하는 Session Key 값 K
- K = (Yb ^ Xa) % p = (64 ^ 28) % 100 = 374144419156711147060143317175368453031918731001856 % 100 = 56
- b가 산출하는 Session Key 값 K
- K = (Ya ^ Xb) % p = (36 ^ 33) % 100 = 2280250319867037997421842330085227917956272625811456 % 100 = 56
- a가 산출하는 Session Key 값 K
- Diffie-Hellman 방식에 의한 키 분배 방법을 이용하여 a와 b는 결과적으로 Session Key값으로 56을 공유하게 됩니다.
1.3. IPSEC에서의 IKE(Internet Key Exchange) 과정에서 사용되는 MODP
IPSEC에서의 IKE(Internet Key Exchange) 과정에 사용되는 미리 알려져야 하는 p(prime modulus)와 g(generator)값은 "RFC3526 - More Modular Exponential (MODP) Diffie-Hellman groups for Internet Key Exchange (IKE)"에서 정의되어 있습니다.
RFC3526 - More Modular Exponential (MODP) Diffie-Hellman groups for Internet Key Exchange (IKE)"에서 정의되어 있습니다.
- 768-bit MODP Group 1
p = 2^768 - 2^704 - 1 + 2^64 * { [2^638 pi] + 149686 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A63A3620 FFFFFFFF FFFFFFFF g = 2 - 1024-bit MODP Group 2
p = 2^1024 - 2^960 - 1 + 2^64 * { [2^894 pi] + 129093 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE65381 FFFFFFFF FFFFFFFF g = 2 - 1536-bit MODP Group 5
p = 2^1536 - 2^1472 - 1 + 2^64 * { [2^1406 pi] + 741804 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F 83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D 670C354E 4ABC9804 F1746C08 CA237327 FFFFFFFF FFFFFFFF g = 2 - 2048-bit MODP Group 14
p = 2^2048 - 2^1984 - 1 + 2^64 * { [2^1918 pi] + 124476 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F 83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D 670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9 DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510 15728E5A 8AACAA68 FFFFFFFF FFFFFFFF g = 2 - 3072-bit MODP Group 15
p = 2^3072 - 2^3008 - 1 + 2^64 * { [2^2942 pi] + 1690314 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F 83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D 670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9 DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510 15728E5A 8AAAC42D AD33170D 04507A33 A85521AB DF1CBA64 ECFB8504 58DBEF0A 8AEA7157 5D060C7D B3970F85 A6E1E4C7 ABF5AE8C DB0933D7 1E8C94E0 4A25619D CEE3D226 1AD2EE6B F12FFA06 D98A0864 D8760273 3EC86A64 521F2B18 177B200C BBE11757 7A615D6C 770988C0 BAD946E2 08E24FA0 74E5AB31 43DB5BFC E0FD108E 4B82D120 A93AD2CA FFFFFFFF FFFFFFFF g = 2 - 4096-bit MODP Group 16
p = 2^4096 - 2^4032 - 1 + 2^64 * { [2^3966 pi] + 240904 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F 83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D 670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9 DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510 15728E5A 8AAAC42D AD33170D 04507A33 A85521AB DF1CBA64 ECFB8504 58DBEF0A 8AEA7157 5D060C7D B3970F85 A6E1E4C7 ABF5AE8C DB0933D7 1E8C94E0 4A25619D CEE3D226 1AD2EE6B F12FFA06 D98A0864 D8760273 3EC86A64 521F2B18 177B200C BBE11757 7A615D6C 770988C0 BAD946E2 08E24FA0 74E5AB31 43DB5BFC E0FD108E 4B82D120 A9210801 1A723C12 A787E6D7 88719A10 BDBA5B26 99C32718 6AF4E23C 1A946834 B6150BDA 2583E9CA 2AD44CE8 DBBBC2DB 04DE8EF9 2E8EFC14 1FBECAA6 287C5947 4E6BC05D 99B2964F A090C3A2 233BA186 515BE7ED 1F612970 CEE2D7AF B81BDD76 2170481C D0069127 D5B05AA9 93B4EA98 8D8FDDC1 86FFB7DC 90A6C08F 4DF435C9 34063199 FFFFFFFF FFFFFFFF g = 2 - 6144-bit MODP Group 17
p = 2^6144 - 2^6080 - 1 + 2^64 * { [2^6014 pi] + 929484 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F 83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D 670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9 DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510 15728E5A 8AAAC42D AD33170D 04507A33 A85521AB DF1CBA64 ECFB8504 58DBEF0A 8AEA7157 5D060C7D B3970F85 A6E1E4C7 ABF5AE8C DB0933D7 1E8C94E0 4A25619D CEE3D226 1AD2EE6B F12FFA06 D98A0864 D8760273 3EC86A64 521F2B18 177B200C BBE11757 7A615D6C 770988C0 BAD946E2 08E24FA0 74E5AB31 43DB5BFC E0FD108E 4B82D120 A9210801 1A723C12 A787E6D7 88719A10 BDBA5B26 99C32718 6AF4E23C 1A946834 B6150BDA 2583E9CA 2AD44CE8 DBBBC2DB 04DE8EF9 2E8EFC14 1FBECAA6 287C5947 4E6BC05D 99B2964F A090C3A2 233BA186 515BE7ED 1F612970 CEE2D7AF B81BDD76 2170481C D0069127 D5B05AA9 93B4EA98 8D8FDDC1 86FFB7DC 90A6C08F 4DF435C9 34028492 36C3FAB4 D27C7026 C1D4DCB2 602646DE C9751E76 3DBA37BD F8FF9406 AD9E530E E5DB382F 413001AE B06A53ED 9027D831 179727B0 865A8918 DA3EDBEB CF9B14ED 44CE6CBA CED4BB1B DB7F1447 E6CC254B 33205151 2BD7AF42 6FB8F401 378CD2BF 5983CA01 C64B92EC F032EA15 D1721D03 F482D7CE 6E74FEF6 D55E702F 46980C82 B5A84031 900B1C9E 59E7C97F BEC7E8F3 23A97A7E 36CC88BE 0F1D45B7 FF585AC5 4BD407B2 2B4154AA CC8F6D7E BF48E1D8 14CC5ED2 0F8037E0 A79715EE F29BE328 06A1D58B B7C5DA76 F550AA3D 8A1FBFF0 EB19CCB1 A313D55C DA56C9EC 2EF29632 387FE8D7 6E3C0468 043E8F66 3F4860EE 12BF2D5B 0B7474D6 E694F91E 6DCC4024 FFFFFFFF FFFFFFFF g = 2 - 8192-bit MODP Group 18
p = 2^8192 - 2^8128 - 1 + 2^64 * { [2^8062 pi] + 4743158 } = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1 29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245 E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F 83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D 670C354E 4ABC9804 F1746C08 CA18217C 32905E46 2E36CE3B E39E772C 180E8603 9B2783A2 EC07A28F B5C55DF0 6F4C52C9 DE2BCBF6 95581718 3995497C EA956AE5 15D22618 98FA0510 15728E5A 8AAAC42D AD33170D 04507A33 A85521AB DF1CBA64 ECFB8504 58DBEF0A 8AEA7157 5D060C7D B3970F85 A6E1E4C7 ABF5AE8C DB0933D7 1E8C94E0 4A25619D CEE3D226 1AD2EE6B F12FFA06 D98A0864 D8760273 3EC86A64 521F2B18 177B200C BBE11757 7A615D6C 770988C0 BAD946E2 08E24FA0 74E5AB31 43DB5BFC E0FD108E 4B82D120 A9210801 1A723C12 A787E6D7 88719A10 BDBA5B26 99C32718 6AF4E23C 1A946834 B6150BDA 2583E9CA 2AD44CE8 DBBBC2DB 04DE8EF9 2E8EFC14 1FBECAA6 287C5947 4E6BC05D 99B2964F A090C3A2 233BA186 515BE7ED 1F612970 CEE2D7AF B81BDD76 2170481C D0069127 D5B05AA9 93B4EA98 8D8FDDC1 86FFB7DC 90A6C08F 4DF435C9 34028492 36C3FAB4 D27C7026 C1D4DCB2 602646DE C9751E76 3DBA37BD F8FF9406 AD9E530E E5DB382F 413001AE B06A53ED 9027D831 179727B0 865A8918 DA3EDBEB CF9B14ED 44CE6CBA CED4BB1B DB7F1447 E6CC254B 33205151 2BD7AF42 6FB8F401 378CD2BF 5983CA01 C64B92EC F032EA15 D1721D03 F482D7CE 6E74FEF6 D55E702F 46980C82 B5A84031 900B1C9E 59E7C97F BEC7E8F3 23A97A7E 36CC88BE 0F1D45B7 FF585AC5 4BD407B2 2B4154AA CC8F6D7E BF48E1D8 14CC5ED2 0F8037E0 A79715EE F29BE328 06A1D58B B7C5DA76 F550AA3D 8A1FBFF0 EB19CCB1 A313D55C DA56C9EC 2EF29632 387FE8D7 6E3C0468 043E8F66 3F4860EE 12BF2D5B 0B7474D6 E694F91E 6DBE1159 74A3926F 12FEE5E4 38777CB6 A932DF8C D8BEC4D0 73B931BA 3BC832B6 8D9DD300 741FA7BF 8AFC47ED 2576F693 6BA42466 3AAB639C 5AE4F568 3423B474 2BF1C978 238F16CB E39D652D E3FDB8BE FC848AD9 22222E04 A4037C07 13EB57A8 1A23F0C7 3473FC64 6CEA306B 4BCBC886 2F8385DD FA9D4B7F A2C087E8 79683303 ED5BDD3A 062B3CF5 B3A278A6 6D2A13F8 3F44F82D DF310EE0 74AB6A36 4597E899 A0255DC1 64F31CC5 0846851D F9AB4819 5DED7EA1 B1D510BD 7EE74D73 FAF36BC3 1ECFA268 359046F4 EB879F92 4009438B 481C6CD7 889A002E D5EE382B C9190DA6 FC026E47 9558E447 5677E9AA 9E3050E2 765694DF C81F56E8 80B96E71 60C980DD 98EDD3DF FFFFFFFF FFFFFFFF g = 2
1.4. 참고사항
- 난수생성
- VPN(Virtual Private Network, 가상사설망)
- 인증서 만들기
- DH(Diffie–Hellman) key exchange(디피-헬만 키 교환, 암호 키를 교환하는 하나의 방법, 두 사람이 암호화되지 않은 통신망을 통해 공통의 비밀 키를 공유할 수 있도록 하는 방법)
- Man-in-the-middle attack
- RSA (cryptosystem, 공개키 암호화 방식의 약칭, 이 암호화 방식의 개발자인 당시 MIT 재학생 Rivest-Shamir-Adelman 3명의 머릿글자)
- https://en.wikipedia.org/wiki/Elliptic-curve_Diffie%E2%80%93Hellman
- Internet Key Exchange (IKE) Attributes
- Internet Key Exchange Version 2 (IKEv2) Parameters
- RFC2409 - The Internet Key Exchange (IKE)
- RFC2412 - The OAKLEY Key Determination Protocol
- RFC2631 - Diffie-Hellman Key Agreement Method
- RFC3526 - More Modular Exponential (MODP) Diffie-Hellman groups for Internet Key Exchange (IKE)
- RFC5114 - Additional Diffie-Hellman Groups for Use with IETF Standards
- RFC6090 - Fundamental Elliptic Curve Cryptography Algorithms
- RFC7748 - Elliptic Curves for Security
- RFC8032 - Edwards-Curve Digital Signature Algorithm (EdDSA)
- RFC8037 - CFRG Elliptic Curve Diffie-Hellman (ECDH) and Signatures in JSON Object Signing and Encryption (JOSE)
- https://wiki.openssl.org/index.php/Diffie_Hellman
- https://nakedsecurity.sophos.com/2015/05/21/anatomy-of-a-logjam-another-tls-vulnerability-and-what-to-do-about-it/
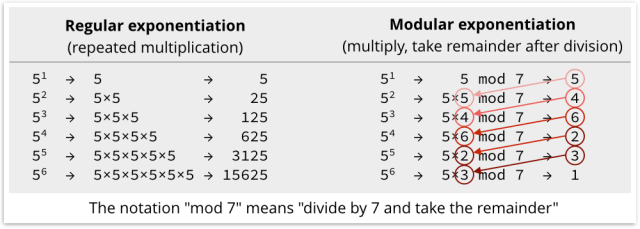
- 특수한 소수 7을 사용하였으며 이를 통해 지수와 나머지값을 찾을 수 있는 방법이 좀더 수월해진다는 것.
[PNG image (24.97 KB)]
- 특수한 소수 7을 사용하였으며 이를 통해 지수와 나머지값을 찾을 수 있는 방법이 좀더 수월해진다는 것.
- Weak Diffie-Hellman and the Logjam Attack
- https://crypto.stackexchange.com/questions/54345/discrete-logarithm-weak-group
- Elliptic Curves: Diffie-Hellman key exchange
Elliptic Curves: Diffie-Hellman key exchange 참고 영상